Graphs

A graph is a structure that shows a relationship (e.g., connection) between two or more objects. Because of their flexibility, graphs are one of the most widely used structures in modern computing. Popular tools and services like online maps, social networks, and even the Internet as a whole are based on how objects relate to one another. In this essay, we’ll highlight the key features of graphs and will demonstrate how to create a basic graph with Swift.

The Basics

As discussed, a graph is a model that shows how objects relate to one another. Graph objects are usually referred to as nodes or vertices. While it would be possible to build and graph a single node, models that contain multiple vertices better represent real-world applications.

Graph objects relate to one other through connections called edges. Depending on your requirements, a vertex could be linked to one or more objects through a series of edges. It's also possible to create a vertex without edges. Here are some basic graph configurations:

An undirected graph with two vertices and one edge.

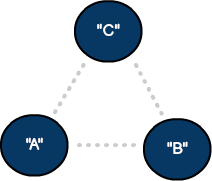
An undirected graph with three vertices and three edges.

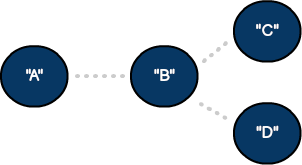
An undirected graph with four vertices and three edges.

Directed vs. Undirected

As shown, there are many ways to configure a graph. An additional option is to set the model to be directed or undirected. The examples above represent undirected graphs. In other words, the connection between vertices A and B is equivalent to the connection between vertices B and A. Social networks are a great example of undirected graphs. Once a request is accepted, both parties (e.g, the sender and recipient) share a mutual connection.

A service like Google Maps is a great example of a directed graph. Unlike an undirected graph, directed graphs only support a one-way connection between source vertices and their destinations. So, for example, vertex A could be connected to B, but A wouldn't necessarily be reachable through B. To show the varying relationship between vertices, directed graphs are drawn with lines and arrows.

Edges & Weights

Regardless of graph type, it's common to represent the level of connectedness between vertices. Normally associated with an edge, the weight is a numerical value tracked for this purpose. As we'll see, modeling of graphs with edge weights can be used to solve a variety of problems.

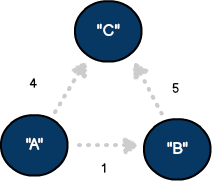
A directed graph with three vertices and three weighted edges.

The Vertex

With our understanding of graphs in place, let's build a basic directed graph with edge weights. To start, here's a data structure that represents a vertex:

//a basic vertex data structure
public class Vertex {
    var key: String?
    var neighbors: Array<Edge>

    init() {
        self.neighbors = Array<Edge>()
    }
}

As we've seen with other structures, the key represents the data to be associated with a class instance. To keep things straightforward, our key is declared as string. In a production app, the key type would be replaced with a generic placeholder, <T>. This would allow the key to store any object like an integer, account or profile.

Adjacency Lists

The neighbors property is an array that represents connections a vertex may have with other vertices. As discussed, a vertex can be associated with one or more items. This list of neighboring items is sometimes called an adjacency list and can be used to solve a variety of problems. Here's a basic data structure that represents an edge:

//a basic edge data structure
public class Edge {
    var neighbor: Vertex
    var weight: Int

    init() {
        weight = 0
        self.neighbor = Vertex()
    }
}

Building The Graph

With our vertex and edge objects built, we can use these structures to construct a graph. To keep things straightforward, we'll focus on the essential operations of adding and configuring vertices.

//a default directed graph canvas
public class SwiftGraph {
    private var canvas: Array<Vertex>
    public var isDirected: Bool

    init() {
        canvas = Array<Vertex>()
        isDirected = true
    }

    //create a new vertex
    func addVertex(key: String) -> Vertex {
        //set the key
        var childVertex: Vertex = Vertex()
        childVertex.key = key

        //add the vertex to the graph canvas
        canvas.append(childVertex)#sthash.bggaFcqw.dpuf

        return childVertex
    }
}

The function addVertex accepts a string which is used to create a new vertex . The SwiftGraph class also has a private property named canvas which is used to manage all vertices. While not required, the canvas can be used to track and manage vertices with or without edges.

Making Connections

Once a vertex is added, it can be connected to other vertices. Here's the process of establishing an edge:

//add an edge to source vertex
func addEdge(source: Vertex, neighbor: Vertex, weight: Int) {
    //create a new edge
    var newEdge = Edge()

    //establish the default properties
    newEdge.neighbor = neighbor
    newEdge.weight = weight

    source.neighbors.append(newEdge)

    //check for undirected graph
    if (isDirected == false) {
        //create a new reversed edge
        var reverseEdge = Edge()

        //establish the reversed properties
        reverseEdge.neighbor = source
        reverseEdge.weight = weight
        neighbor.neighbors.append(reverseEdge)
    }
}

The function addEdge receives two vertices, identifying them as source and neighbor. Since our model defaults to a directed graph, a new edge is created and is added to the adjacency list of the source vertex. For an undirected graph, an additional edge is created and added to the neighbor vertex.

As we've seen, there are many components to graph theory. In the next section, we'll examine a popular problem (and solution) with graphs known as shortest paths.