Binary Search Trees

A binary search tree is a data structure that stores information in the logical hierarchy. As demonstrated with Big O Notation, algorithms provide the best results with sorted data. Binary Search Trees extend this idea by using specific rules. A binary search tree (BST) should not be mistaken for a binary tree or trie. Those structures also store information in a hierarchy, but employ different rules.

How It Works

A binary search tree is comprised of a key and two indicators. The key represents the data you would like to store, such as a string or scalar value. Typically represented with pointers, the indicators store the location (also called the address) of its two children. The left child contains a value that is smaller than its parent. Conversely, the right child contains a value greater than its parent.

The Data Structure

Here's an example of a BST written in Swift. Using generics, the structure also stores any type of object and supports nil values. The concept of combining keys and pointers to create hierarchies not only applies to binary search trees, but to other structures like tries and binary trees.

//generic binary search tree
public class AVLTree<T: Comparable> {
    var key: T?
    var left: AVLTree?
    var right: AVLTree?

    init() {
    }
}

When creating algorithms, it is good practice to set your class properties to nil before they are used. Swift helps to enforce this best-practice at compile time through a new paradigm called Optionals. Along with our class declaration, the generic type contraint <T: Comparable> is also defined to ensure instances conform to a specific protocol.

The Logic

Here's an example of a simple array written in Swift. We'll use this data to build our binary search tree:

//a simple array of unsorted integers
let numberList : Array<Int> = [8, 2, 10, 9, 11, 1, 7]

Here's the same list visualized as a balanced binary search tree. It does not matter that the values are unsorted. Rules governing the BST will place each node in its "correct" position accordingly.

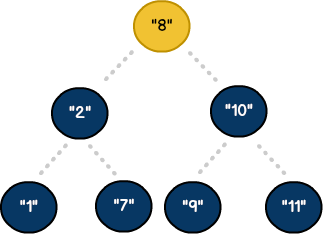
Building The Hierarchy

Here's the class used for creating the BST. Written in Swift, the method addNode employs the rules to position each array value.

public class AVLTree<T: Comparable> {
    var key: T?
    var left: AVLTree?
    var right: AVLTree?

    //add item based on its value
    func addNode(key: T) {
        //check for the head node
        if (self.key == nil) {
            self.key = key
            return
        }

        //check the left side of the tree
        if (key < self.key) {
            if (self.left != nil) {
                left!.addNode(key)#sthash.3jVtGzNq.dpuf
            }
            else {
                //create a new left node
                var leftChild : AVLTree = AVLTree()
                leftChild.key = key
                self.left = leftChild
            }
        } //end if

        //check the left side of the tree
        if (key > self.key) {
            if (self.right != nil) {
                right!.addNode(key)
            }
            else {
                //create a new right node
                var rightChild : AVLTree = AVLTree()
                rightChild.key = key
                self.right = rightChild
            }
        } //end if
    } //end function
} //end class

The method addNode uses recursion to determine where data is added. While not required, recursion is a powerful enabler as each child becomes another instance of a BST. As a result, inserting data becomes a straightforward process of iterating through the array.

//a simple array of unsorted integers
let numberList : Array<Int> = [8, 2, 10, 9, 11, 1, 7]

//create a new BST instance
var root = AVLTree<Int>()

//sort each item in the list
for number in numberList {
    root.addNode(number)
}

Efficiency

BSTs are powerful due to their consistent rules. However, their greatest advantage is speed. Since data is organized at the time of insertion, a clear pattern emerges. Values less than the "root" node (e.g 8) will naturally filter to the left. Conversely, all values greater than the root will filter to the right.

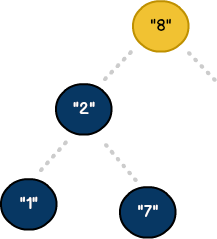
As we saw with Big O Notation, our understanding of the data allows us to create an effective algorithim. So, for example, if we were searching for the value 7, its only required that we traverse the left side of the BST. This is due to our search value being smaller than our root node (e.g 8). Binary Search Trees typically provide O(log n) for insertion and lookup. Algorithms with an efficiency of O(log n) are said to run in logarithmic time.