Stacks & Queues

Stacks) and queues) are structures that help organize data in a particular order. Their concept is based on the idea that information can be organized similar to how things interact in the real world. For example, a stack of kitchen plates can be represented by placing a single plate on a group of existing plates. Similarly, a queue can be easily understood by observing groups of people waiting in a line at a concert or grand opening.

In computer science, the idea of stacks and queues can be seen in numerous ways. Any app that makes use of a shopping cart, waiting list or playlist employs a stack or queue. In programming, a call stack is often used as an essential debugging and analytics tool. For this essay, we'll discuss the idea of stacks and queues and will review how to implement a queue in code.

How it works

In their basic form, stacks and queues employ the same structure and only vary in their use. The data structure common to both forms is the linked list. Using generics, we'll build a queue to hold any type of object. In addition, the class will also support nil values. We'll see the significance of these details as we create additional components.

//generic queue data object
class QNode<T> {
    var key: T?
    var next: QNode?
}

The Concept

Along with our data structure, we'll implement a factory class for managing items. As shown, queues support the concept of adding and removal along with other supportive functions.

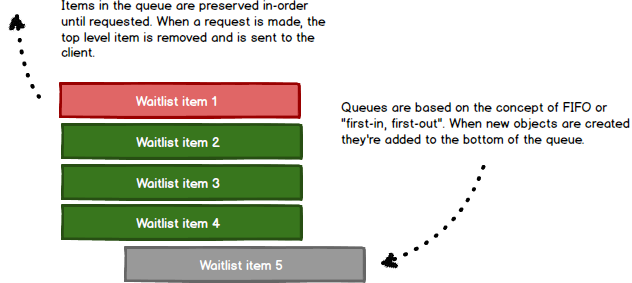
Enqueuing Objects

The process of adding items is often referred to as 'enqueuing'. Here, we define the method to enqueue objects as well as the property top that will serve as our queue list.

public class Queue<T> {
    private var top: QNode<T>! = QNode<T>()

    //enqueue the specified object
    func enQueue(var key: T) {
        //check for the instance
        if (top == nil) {
            top = QNode<T>()
        }

        //establish the top node
        if (top.key == nil) {
            top.key = key;
            return
        }

        var childToUse: QNode<T> = QNode<T>()
        var current: QNode = top

        //cycle through the list of items to get to the end.
        while (current.next != nil) {
            current = current.next!
        }

        //append a new item
        childToUse.key = key;
        current.next = childToUse;
    }
}

The process to enqueue items is similar to building a generic linked list. However, since queued items can be removed as well as added, we must ensure that our structure supports the absence of values (e.g. nil). As a result, the class property top is defined as an implicit unwrapped optional.

To keep the queue generic, the enQueue method signature also has a parameter that is declared as type T. With Swift, generics not only preserves type information but also ensures objects conform to various protocols.

Dequeueing Objects

Removing items from the queue is called dequeuing. As shown, dequeueing is a two-step process that involves returning the top-level item and reorganizing the queue.

//retrieve items from the top level in O(1) constant time
func deQueue() -> T? {
    //determine if the key or instance exists
    let topitem: T? = self.top?.key

    if (topitem == nil) {
        return nil
    }

    //retrieve and queue the next item
    var queueitem: T? = top.key!

    //use optional binding
    if let nextitem = top.next {
        top = nextitem
    }
    else {
        top = nil
    }

    return queueitem
}

When dequeuing, it is vital to know when values are absent. For the method deQueue, we account for the potential absence of a key in addition to an empty queue (e.g. nil). In Swift, one must use specific techniques like optional chaining to check for nil values.

Supporting Functions

Along with adding and removing items, important supporting functions include checking for an empty queue as well as retrieving the top level item.

//check for the presence of a value
func isEmpty() -> Bool {
    //determine if the key or instance exist
    if let topitem: T = self.top?.key {
        return false
    }
    else {
        return true
    }
}

//retrieve the top most item
func peek() -> T? {
    return top.key!
}

Efficiency

In this example, our queue provides O(n) for insertion and O(1) for lookup. As noted, stacks support the same basic structure but generally provide O(1) for both storage and lookup. Similar to linked lists, stacks and queues play an important role when managing other data structures and algorithms.