Tries

Similar to binary search trees, trie data structures also organize information in a logical hierarchy. Often pronounced "try", the term comes from the English language verb to "retrieve". While most algorithms are designed to manipulate generic data, tries are commonly used with strings. In this essay, we'll review trie structures and will implement our own trie model with Swift.

How it works

As discussed, tries organize data in a hierarchy. To see how they work, let's build a dictionary that contains the following words:

Ball
Balls
Ballard
Bat
Bar
Cat
Dog

At first glance, we see words prefixed with the phrase "Ba", while entries like "Ballard" combine words and phrases (e.g., "Ball" and "Ballard"). Even though our dictionary contains a limited quantity of words, a thousand-item list would have the same properties. Like any algorithm, we'll apply our knowledge to build an efficient model. To start, let's create a new trie for the word "Ball":

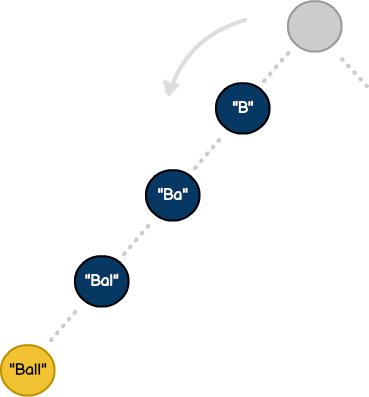
Tries involve building hierarchies, storing phrases along the way until a word is created (seen in yellow). With so many permutations, it's important to know what qualifies as an actual word. For example, even though we've stored the phrase "Ba", it's not identified as a word. To see the significance, consider the next example:

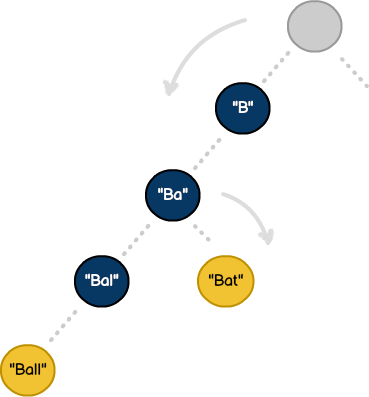
As shown, we've traversed the structure to store the word "Bat". The trie has allowed us to reuse the permutations of "B" and "Ba" added by the inclusion of the word "Ball". Though most algorithms are measured on time efficiency, tries demonstrate great efficiency with time and space. Practical implementations of tries can be seen in modern software features like auto-complete, search engines and spellcheck.

The Data Structure

Here's an example of a trie data structure written in Swift. In addition to storing a key, the structure also includes an Array for identifying its children. Unlike a binary search tree, a trie can store an unlimited number of leaf nodes. The boolean value isFinal will allow us to distinguish words and phrases. Finally, the level will indicate the node's level in a hierarchy.

//generic trie data structure
public class TrieNode {
    var key: String!
    var children: Array<TrieNode>
    var isFinal: Bool
    var level: Int

    init() {
        self.children = Array<TrieNode>()
        self.isFinal = false
        self.level = 0
    }
}

Adding Words

Here's an algorithm that adds words to a trie. Although most tries are recursive#Recursive_functions_and_algorithms) structures, our example employs an iterative technique. The while loop compares the keyword length with the current node's level. If no match occurs, it indicates additional keyword phases remain to be added.

//generic trie implementation
public class Trie {
    private var root: TrieNode!

    init(){
        root = TrieNode()
    }

    //builds a recursive tree of dictionary content
    func addWord(keyword: String) {
        if (keyword.length == 0){
            return;
        }

        var current: TrieNode = root
        var searchKey: String!

        while(keyword.length != current.level) {
            var childToUse: TrieNode!
            var searchKey = keyword.substringToIndex(current.level + 1)

            //iterate through the node children
            for child in current.children {
                if (child.key == searchKey) {
                    childToUse = child
                    break
                }
            }

            //create a new node
            if (childToUse == nil) {
                childToUse = TrieNode()
                childToUse.key = searchKey
                childToUse.level = current.level + 1;
                current.children.append(childToUse)
            }

            current = childToUse
        } //end while

        //add final end of word check
        if (keyword.length == current.level) {
            current.isFinal = true
            println("end of word reached!")
            return;
        }
    } //end function
}

A final check confirms our keyword after completing the while loop. As part of this, we update the current node with the isFinal indicator. As mentioned, this step will allow us to distinguish words from phrases.

Finding Words

The algorithm for finding words is similar to adding content. Again, we establish a while loop to navigate the trie hierarchy. Since the goal will be to return a list of possible words, these will be tracked using an Array.

//find all words based on a prefix
func findWord(keyword: String) -> Array<String>! {
    if (keyword.length == 0){
        return nil
    }

    var current: TrieNode = root
    var searchKey: String!
    var wordList: Array<String>! = Array<String>()

    while(keyword.length != current.level) {
        var childToUse: TrieNode!
        var searchKey = keyword.substringToIndex(current.level + 1)

        //iterate through any children
        for child in current.children {
            if (child.key == searchKey) {
                childToUse = child
                current = childToUse
                break
            }
        }

        //prefix not found
        if (childToUse == nil) {
            return nil
        }
    } //end while

    //retrieve keyword and any decendants
    if ((current.key == keyword) && (current.isFinal)) {
        wordList.append(current.key)
    }

    //add children that are words
    for child in current.children {
        if (child.isFinal == true) {
            wordList.append(child.key)
        }
    }
    return wordList
} //end function

The findWord function checks to ensure keyword phrase permutations are found. Once the entire keyword is identified, we start the process of building our word list. In addition to returning keys identified as words (e.g., "Bat", "Ball"), we account for the possibility of returning nil by returning an implicit unwrapped optional.

Extending Swift

Even though we've written our trie in Swift, we've extended some language features to make things work. Commonly known as "categories" in Objective-C, our algorithms employ two additional Swift "extensions". The following class extends the functionality of the native String class:

//extend the native String class
extension String {
    //compute the length of string
    var length: Int {
        return Array(self).count
    }

    //returns characters of a string up to a specified index
    func substringToIndex(to: Int) -> String {
        return self.substringToIndex(advance(self.startIndex, to))
    }
}