Tree Balancing

In the previous essay, we saw how binary search trees (BST) are used to manage data. With basic logic, an algorithm can easily traverse a model, searching data in O(log n) time. However, there are occasions when navigating a tree becomes inefficient - in some cases working at O(n) time. In this essay, we wil review those scenarios and introduce the concept of tree balancing.

New Models

To start, let's revisit our original example. Array values from numberList were used to build a tree. As shown, all nodes had either one or two children - otherwise called leaf nodes. This known as a balanced binary search tree.

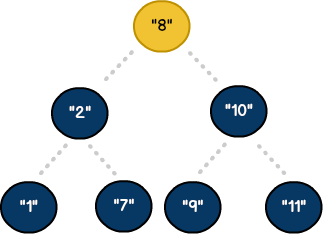
Our model achieved balance not only through usage of the addWord algorithm, but also by the way keys were inserted. In reality, there could be numerous ways to populate a tree. Without considering other factors, this can produce unexpected results:

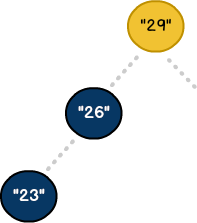
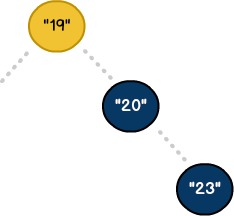
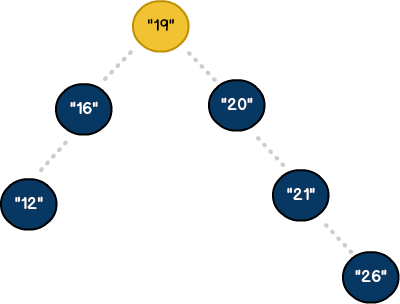
New Heights

To compensate for these imbalances, we need to expand the scope of our algorithm. In addition to left / right logic, we'll add new property called height. Coupled with specific rules, we can use height to detect tree imbalances. To see how this works, let's create a new BST:

//a simple array of unsorted integers
let balanceList : Array<Int> = [29, 26, 23]

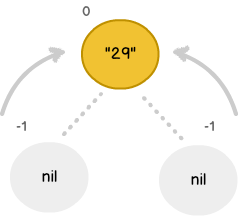
To start, we add the root node. As the first item, left / right leaves don't yet exist so they are initialized to nil. Arrows point from the leaf nodes to the root because they are used to calculate its height. For math purposes, the height of non-existent leaves are set to -1.

With a model in place, we can calculate the node's height. This is done by comparing the height of each leaf, finding the largest value, then increasing that value by +1. For the root node this equates to 0. In Swift, these rules can be represented as follows:

//retrieve the height of a node
func getNodeHeight(aNode: AVLTree!) -> Int {
    if (aNode == nil) {
        return -1
    }
    else {
        return aNode.height
    }
}

//calculate the height of a node
func setNodeHeight() -> Bool {
    //check for a nil condition
    if (self.key == nil) {
        println("no key provided..")
        return false
    }

    //set height variable
    var nodeHeight: Int = 0

    //compare and calculate node height
    nodeHeight = max(getNodeHeight(self.left), getNodeHeight(self.right)) + 1

    self.height = nodeHeight

    return true
}

Measuring Balance

With the root node established, we can proceed to add the next value. Upon implementing standard BST logic, item 26 is positioned as the left leaf node. As a new item, its height is also calculated (i.e., 0). However, since our model is a hierarchy, we traverse upwards to recalculate its parent height value.

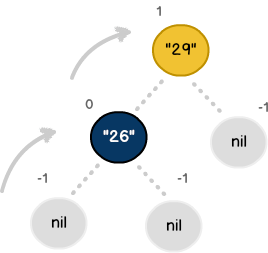
With multiple nodes present, we run an additional check to see if the BST is balanced. In computer science, a tree is considered balanced if the height difference between its leaf nodes is less than 2. As shown below, even though no right-side items exist, our model is still valid.

//example math for tree balance check
var rootVal: Int!
var leafVal: Int!

leafVal = abs((-1) - (-1)) //equals 0 (balanced)
rootVal = abs((0) - (-1)) //equals 1 (balanced)

In Swift, these nodes can be checked with the isTreeBalanced method.

//determine if the tree is balanced
func isTreeBalanced() -> Bool {
    //check for a nil condition
    if (self.key == nil) {
        println("no key provided..")
        return false
    }

    //use absolute value to calculate right / left imbalances
    if (abs(getNodeHeight(self.left) - getNodeHeight(self.right)) <= 1) {
        return true
    }
    else {
        return false
    }
} //end function

Adjusting the Model

With 29 and 26 added can proceed to insert the final value (i.e., 23). Like before, we continue to traverse the left side of the tree. However, upon insertion, the math reveals node 29 violates the BST property. In other words, its subtree is no longer balanced.

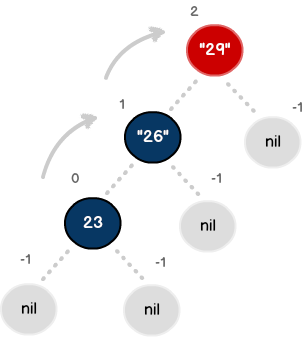
//example math for tree balance check
var rootVal: Int!
rootVal = abs((1) - (-1)) //equals 2 (unbalanced)

For the tree to maintain its BST property, we need change its performance from O(n) to O(log n). This can be achieved through a process called rotation. Since the model has more nodes to the left, we'll balance it by performing a right rotation sequence. Once complete, the new model will appear as follows:

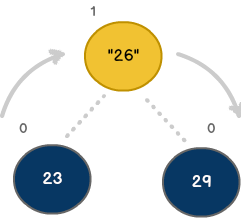
As shown, we've been able to rebalance the BST by rotating the model to the right. Originally set as the root, node 29 is now positioned as the right leaf. In addition, node 26 has been moved to the root. In Swift, these changes can be achieved with the following:

//right rotation sequence
var childToUse: AVLTree = AVLTree()
childToUse.height = 0
childToUse.key = self.key

if (getNodeHeight(self.left) - getNodeHeight(self.right) > 1) {
    //reset the root node
    self.key = self.left?.key
    self.height = getNodeHeight(self.left)

    //assign the new right node
    self.right = childToUse

    //adjust the left node
    self.left = self.left?.left
    self.left?.height = 0
}

Even though we undergo a series of steps, the process occurs in O(1) time. Meaning, its performance is unaffected by other factors such as number of leaf nodes, descendants or tree height. In addition, even though we've completed a right rotation, similar steps could be implemented to resolve both left and right imbalances.

The Results

With tree balancing, it is important to note that techniques like rotations improve performance, but do not change tree output. For example, even though a right rotation changes the connections between nodes, the overall BST sort order is preserved. As a test, one can traverse a balanced and unbalanced BST (comparing the same values) and receive the same results. In our case, a simple depth-first search will produce the following:

//sorted values from a traversal
23, 26, 29