Big O Notation

Building a service that finds information quickly could mean the difference between success and failure. For example, much of Google's success comes from algorithms that allow people to search vast amounts of data with great efficiency.

There are numerous ways to search and sort data. As a result, computer scientists have devised a way for us to compare the efficiency of software algorithms regardless of computing device, memory or hard disk space. Asymptotic analysis is the process of describing the efficiency of algorithms as their input size (n) grows. In computer science, asymptotics are usually expressed in a common format known as Big O Notation.

Making Comparisons

To understand Big O Notation one only needs to start comparing algorithms. In this example, we compare two techniques for searching values in a sorted array.

//a simple array of sorted integers 
let numberList : Array<Int> = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Linear Time - O(n)

Our first approach employs a common "brute force" technique that involves looping through the entire array until we find a match. In Swift, this can be achieved with the following;

//brute force approach - O(n) linear time
func linearSearch(key: Int) {

    //check all possible values until we find a match
    for number in numberList {
        if (number == key) {
            let results = "value \(key) found.."
            break
        }
    }
}

While this approach achieves our goal, each item in the array must be evaluated. A function like this is said to run in "linear time" because its speed is dependent on its input size. In other words, the algorithm become less efficient as its input size (n) grows.

Logarithmic Time - O(log n)

Our next approach uses a technique called binary search. With this method, we apply our knowledge about the data to help reduce our search criteria.

//the binary approach - O(log n) logarithmic time
func binarySearch(key: Int, imin: Int, imax: Int) {

    //find the value at the middle index
    var midIndex : Double = round(Double((imin + imax) / 2))
    var midNumber = numberList[Int(midIndex)]

    //use recursion to reduce the possible search range
    if (midNumber > key ) {
        binarySearch(key, imin, Int(midIndex) - 1)
    }
    else if (midNumber < key ) {
        binarySearch(key, Int(midIndex) + 1, imax)
    }
    else {
        let results = "value \(key) found.."
    }
} //end func

To recap, we know we're searching a sorted array to find a specific value. By applying our understanding of data, we assume there is no need to search values less than than the key. For example, to find the value at index 8, it would be impossible to find that value at array index 0 - 7.

By applying this logic we substantially reduce the amount of times the array is checked. This type of search is said to work in "logarithmic time" and is represented with the symbol O(log n). Overall, its complexity is minimized when the size of its inputs (n) grows. Here's a table that compares their performance;

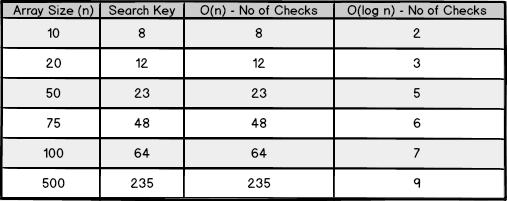
Plotted on a graph, it's easy to compare the running time of popular search and sorting techniques. Here, we can see how most algorithms have relatively equal performance with small datasets. It's only when we apply large datasets that we're able to see clear differences.

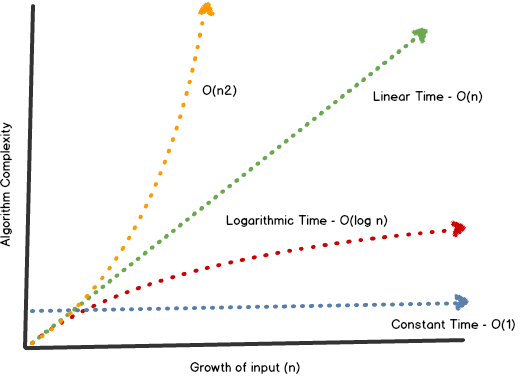
Not familiar with logarithms? Here's a great Khan Academy video that demonstrates how this works.